Mathematical Modeling as a Tool in the Fight Against Malaria The study of infectious disease epidemiology has had a fairly long history. For several hundred years, scientists have studied disease outbreaks. Notably, Ronald Ross and Daniel Bernoulli produced various models to accurately predict and track the spread of infections throughout a human population. These models, which were applied to diseases such as smallpox and plague, took into account several important features of the outbreak including the number of people infected and the percentage of the vector (the insect that transmits a disease to humans) containing the actual pathogen. One of the most prominent diseases to which models have been applied is malaria, which is caused by the protozoan Plasmodium. Dr. John Marshall, assistant professor in the School of Public Health at the University of California, Berkeley, has for several years been using modeling to predict the outcomes of certain control strategies for malaria. Malaria follows many general rules used in non-specific modeling of disease transmission (see Figure 1), but has some unique aspects like incubation period (the time in which the parasite needs to grow inside the mosquito). The models account for host parameters including whether the patient is symptomatic, the patient’s immunity and the patterns of how people travel. This last tenet is especially important as human population movement affects how malaria itself actually spreads. Vector parameters contribute to the model as well, such as how long the mosquito lives and its sensitivity to climate and geography. Ultimately, the model can be tested against data from a real outbreak and then tweaked to fit the data more precisely. 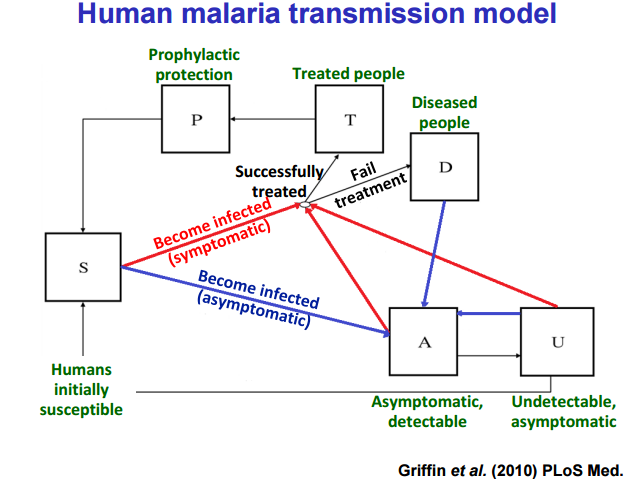 Figure 1: Complexity of the Malarial Transmission Model. This diagram represents the factors that must be accounted for when making predictions about the spread of malaria through human populations. Important factors include whether the patient shows symptoms that doctors can see and if the patient can be treated in time. 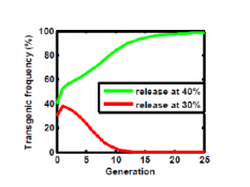 Figure 2: Differential Outcomes of the Semele System as a Function of Initial Introduction Frequency The Semele transgenic system relies on a transgenic male-specific seminal toxin and a female-specific antidote. Whether these mosquitoes proliferate into a stable population, after initial introduction, depends on how many are released at the beginning. Although modeling is an integral tool in the investigation of disease transmission and outbreak, treatments offer a proactive solution. Successful methods include vaccinations and bed netting treated with insecticide. However, modeling can be used to test novel control strategies before actual implementation. Specifically, Dr. Marshall and his colleagues are interested in how the introduction of certain types of genetically modified mosquitoes could impact the wild mosquito population, and ultimately, whether they will result in malaria reduction or elimination. Several transgenic mosquito systems, such as the X-Shredder, Medea and Semele (see figure 2), operate by introducing genetically modified mosquitoes into a natural population to propagate selected genes. The goal of these systems is to reduce the numbers of mosquitoes that can transmit disease by either reducing the number of viable offspring or by killing off the adult population. One of the advantages of these systems is that they have limited, if any, non-target effects on other species, since pesticide use is not implemented. However, there are some limitations to the models that Dr. Marshall and his colleagues use, which impact the full potential of this approach to malaria control. Pesticide resistance is most notable among these, and obtaining an accurate picture of this can be difficult at best. Several human elements are also difficult to account for, such as how many people actually use preventive methods like vaccinations and treated bed nets, whether due to personal choice or because of community or political influences and priorities. The ability to model and treat disease is priceless in the fight against infectious outbreaks. Enhanced application of old techniques and novel genetic-based systems provide multiple avenues towards maintenance, and possibly elimination, of these diseases. Complex models are also indispensable for achieving this goal. Past experience has shown that eliminating a particular disease is entirely possible. The future, therefore, promises to hold similar if not greater success. Additionally, community perception of a control measure plays a significant role in its success. Some of Dr. Marshall’s recent work involved surveying village residents in Mali, West Africa to assess their perception and reception of genetically modified mosquitoes. His work suggests that residents would be receptive to using genetically modified mosquitoes as a control measure in their village if it had been shown to work elsewhere. About the Authors: Justin Rosenthal is a fourth year Doctoral Student in the University of Maryland’s Entomology Department. His interests mainly concern the influence of particular regulatory factors, namely those related to RNA processing, on cell development within the context of the insect central nervous system. Jennifer Jones is a first year Doctoral Student at the University of Maryland, studying mosquito populations along a socioeconomic gradient in Baltimore. Comments are closed.
|
Categories
All
Archives
June 2024
|
RSS Feed
